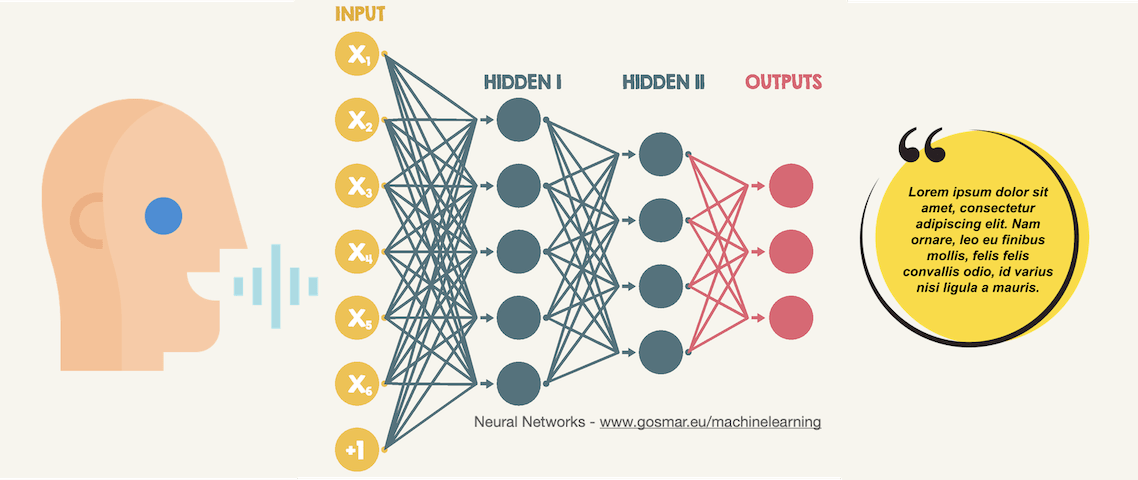
Deep-learning ASR convolutional-neural-networks
Oggi vediamo un esempio di CNN (reti neurali convoluzionali) applicato al riconoscimento vocale (speech recognition).
Obiettivo del nostro modello di machine learning basato su algoritmi CNN di Deep Learning sarà quello di riuscire a classificare alcune parole semplici, iniziando dai numeri da zero a nove.
Per estrarre delle caratteristiche distintive del parlato adotteremo prima una procedura di codifica della voce piuttosto utilizzata in ambito ASR (Automatic Speech Recognition) denominata Mel Frequency Cepstral Coefficient o più semplicemente MFCC.
Grazie alla tecnica MFCC saremo in grado di codificare ogni singola parola pronunciata vocalmente in una sequenza di vettori ognuno dei quali lungo 13: i coefficienti ottenuti con l’algoritmo MFCC.
Nel nostro caso – essendo le singole parole rappresentate da numeri di una sola cifra – andremo per semplicità a codificare ogni singolo numero con una matrice 48 x 13.
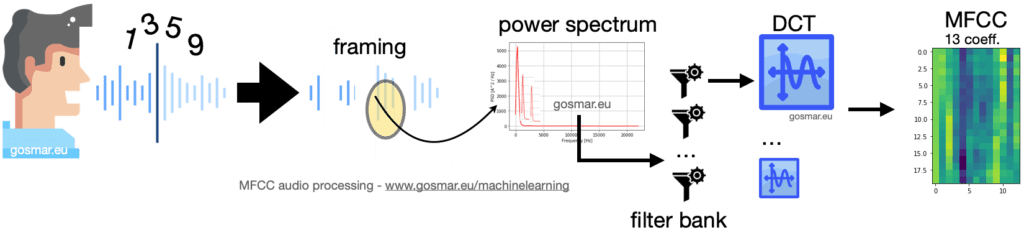
L’immagine precedente mostra la catena dei principali moduli coinvolti in un processo di codifica MFCC: il segnale vocale viene segmentato in più frame di durata adeguata nel dominio del tempo (generalmente 25-40 ms).
Per ognuno di questi segmenti andiamo a calcolare la trasformata in frequenza e quindi lo spettro di potenza.
Il risultato è fornito in input a una serie di filtri parzialmente sovrapposti (filter bank) che calcolano la densità spettrale di energia corrispondenti a differenti intervalli di frequenza del nostro spettro di potenza.
Per ogni frame temporale, si ottengono così 26 coefficienti che sono costituiti dal risultato dello spettro energetico a valle di ciascun filtro. Il risultato viene infine processato tramite la trasformata discreta del coseno o DCT (Discrete Cosine Transform).
La DCT ha la proprietà di riuscire a codificare le feature di un segnale utilizzando al meglio le basse frequenze, caratteristica per noi utile visto che abbiamo a che fare con un segnale vocale, le cui proprietà principali sono comprese tra i 300 e 3400 Hz circa.
Risultato finale: a valle di questo processo, la MFCC ci fornisce 13 coefficienti utili (si prendono i primi 13 del 26 complessivi) che andremo a utilizzare con opportuni algoritmi di machine learning che sfruttano classificatori ottimali (in questo esempio basati su CNN).
Per l’apprendimento del classificatore utilizzeremo il dataset qui disponibile relativo al Free Spoken Digit Dataset: si tratta di circa 2000 registrazioni vocali effettuate con differenti persone che hanno pronunciato i numeri da zero a nove in diverse situazioni ambientali e temporali.
Come classificatore utilizzeremo la rete neurale convoluzionale a diversi livelli che possiamo schematizzare nella figura seguente.
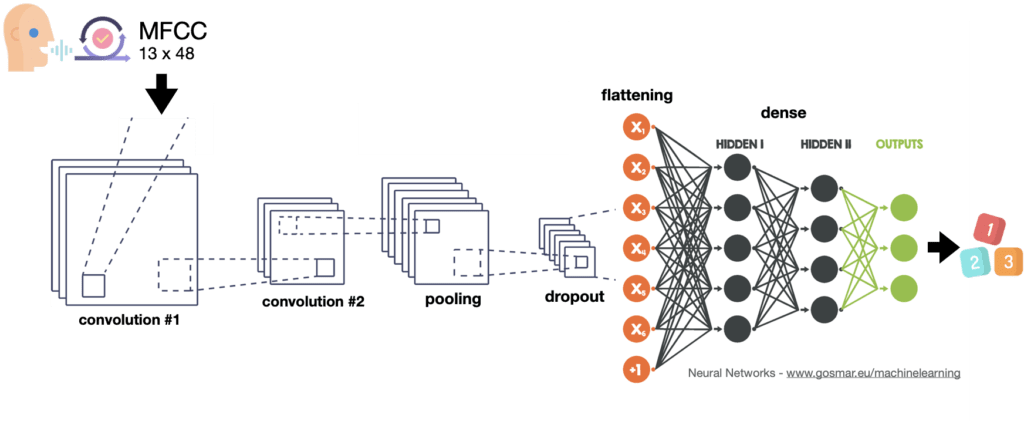
Vediamo ora un po’ di codice e le performance!
Importiamo alcune librerie utili in Python:
import pandas as pd
from sklearn.model_selection import train_test_split
import pickle
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
from IPython.display import HTML
import numpy as np
from sklearn import preprocessing
import matplotlib.pyplot as plt
from scipy.io import wavfile as wav
import scipy
from python_speech_features import mfcc
from python_speech_features import logfbank
import tensorflow as tf
from keras.models import Sequential
from keras.layers import Dense, Flatten, Activation, Dropout, LSTM
from keras.layers import Conv2D, MaxPooling2D, GlobalMaxPooling2D
from keras.optimizers import SGD
import os
Analizziamo uno dei messaggi vocali a caso, sia ad esempio il file “0_jackson_0.wav”:
(rate,sig1) = wav.read(“/Users/diego/Diego/Xenialab/AI/jupyter/digits/0_jackson_0.wav”)
N = sig1.shape[0]
L = N / rate
f, ax = plt.subplots()
ax.plot(np.arange(N) / rate, sig1)
ax.set_xlabel(‘Time [s]’)
ax.set_ylabel(‘Amplitude [Base-ten signed range (per sample)]’);
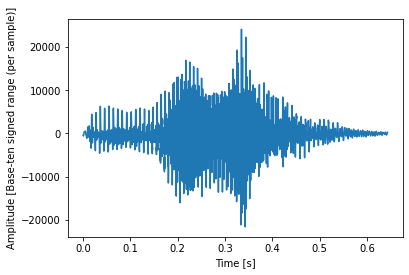
Ora vediamo per curiosità il risultato dell’applicazione della funzione MFCC al segnale:
mfcc_feat = mfcc(sig1,rate,nfft=512)
plt.imshow(mfcc_feat[0:20,:])
Possiamo visualizzare una sorta di spettrogramma: in realtà sono i 13 output della DCT per ogni frame temporale del segnale… qui ne mostriamo i primi venti.
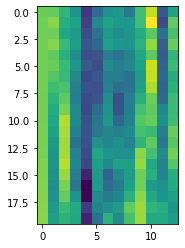
…Possiamo divertirci a visualizzare altri segnali e pronunce varie in modo analogo!
È giunto il momento di iniziare fare le cose sul serio.
Importiamo i 2000 file con le differenti registrazioni vocali in una apposita lista di vettori, che andiamo poi a convertire e separare opportunamente, per ottenere i valori utili all’apprendimento e la target label da predire:
soundfile = os.listdir(‘/Users/diego/Diego/Xenialab/AI/jupyter/digits’)
data=[]
for i in soundfile:
(rate,sig) = wav.read(‘/Users/diego/Diego/Xenialab/AI/jupyter/digits/’+i)
data.append(sig)
#set the independent var
size = 48
X=[]
for i in range(len(data)):
mfcc_feat = mfcc(data[i],rate,nfft=512)
mfcc_feat = np.resize(mfcc_feat, (size,13))
X.append(mfcc_feat)
X = np.array(X)
#set the target label
y = [i[0] for i in soundfile]
Y = pd.get_dummies(y)
La target label non è nient’altro che una matrice che per ognuno dei 2000 file registrati valorizza “1” in corrispondenza del numero pronunciato.
Vediamo le prime tre righe di questa matrice:
print(Y[0:3])
0 1 2 3 4 5 6 7 8 9 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 2 0 0 0 0 1 0 0 0 0 0
Quindi le prime tre registrazioni caricate corrispondono ai numeri cinque, tre e quattro.
Convertiamo la target label in opportuna matrice:
Y = np.array(Y)
Stampiamo anche il formato della variabile indipendente X per comprendere meglio:
print(X.shape)
(2000, 48, 13)
X è quindi composta da 2000 matrici 48 x 13 corrispondente alle feature estratte con la funzione MFCC per ciascuna registrazione vocale.
È venuto il momento di effettuare il processo di apprendimento (training) utilizzando la rete neurale convoluzionale che abbiamo previsto. Visualizziamola nuovamente:
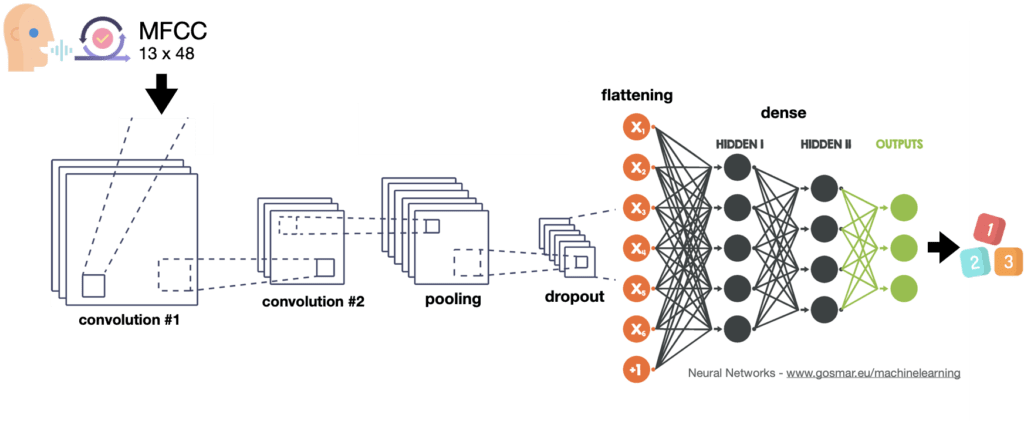
Questo tipo di architettura può essere utilizzato anche per numerose altre applicazioni, tra cui il riconoscimento immagini e classificazioni più disparate. In questo caso applichiamolo per il nostro obiettivo, cioè il riconoscimento vocale.
model = Sequential()
#Convolution layers
model.add(Conv2D(8, (3, 3), activation=’relu’, input_shape=(size, 13,1)))
model.add(Conv2D(8, (3, 3), activation=’relu’))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.1))
#Flattening
model.add(Flatten(input_shape=(size, 13,1)))
#1st fully connected Neural Network hidden-layer
model.add(Dense(64))
model.add(Dropout(0.16))
model.add(Activation(‘relu’))
#2nd fully connected Neural Network hidden-layer
model.add(Dense(64))
model.add(Dropout(0.12))
model.add(Activation(‘relu’))
#Output layer
model.add(Dense(10))
model.add(Activation(‘softmax’))
model.summary()
Model: "sequential_1" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= conv2d_1 (Conv2D) (None, 46, 11, 8) 80 _________________________________________________________________ conv2d_2 (Conv2D) (None, 44, 9, 8) 584 _________________________________________________________________ max_pooling2d_1 (MaxPooling2 (None, 22, 4, 8) 0 _________________________________________________________________ dropout_1 (Dropout) (None, 22, 4, 8) 0 _________________________________________________________________ flatten_1 (Flatten) (None, 704) 0 _________________________________________________________________ dense_1 (Dense) (None, 64) 45120 _________________________________________________________________ dropout_2 (Dropout) (None, 64) 0 _________________________________________________________________ activation_1 (Activation) (None, 64) 0 _________________________________________________________________ dense_2 (Dense) (None, 64) 4160 _________________________________________________________________ dropout_3 (Dropout) (None, 64) 0 _________________________________________________________________ activation_2 (Activation) (None, 64) 0 _________________________________________________________________ dense_3 (Dense) (None, 10) 650 _________________________________________________________________ activation_3 (Activation) (None, 10) 0 ================================================================= Total params: 50,594 Trainable params: 50,594 Non-trainable params: 0
Compiliamo il modello usando l’ottimizzatore SGD:
sgd = SGD(lr=0.01, decay=1e-6, momentum=0.9, nesterov=True)
model.compile(loss=’binary_crossentropy’,
optimizer=sgd,
metrics=[‘accuracy’])
Separiamo i dati di training e di test e rendiamoli della dimensione adeguata per essere riconosciuti come tensori dalla nostra rete CNN:
x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=0.25)
x_train = x_train.reshape(-1, size, 13, 1)
x_test = x_test.reshape(-1, size, 13, 1)
Fittiamo il modello e valutiamo le performance:
history = model.fit(
x_train,
y_train,
epochs=18,
batch_size=32,
validation_split=0.2,
shuffle=True
)
model.evaluate(x_test, y_test, verbose=2)
Train on 1200 samples, validate on 300 samples Epoch 1/18 1200/1200 [==============================] - 1s 469us/step - loss: 0.3319 - accuracy: 0.8967 - val_loss: 0.2683 - val_accuracy: 0.9070 Epoch 2/18 1200/1200 [==============================] - 0s 256us/step - loss: 0.2534 - accuracy: 0.9066 - val_loss: 0.1943 - val_accuracy: 0.9217 ... ... Epoch 18/18 1200/1200 [==============================] - 0s 254us/step - loss: 0.0444 - accuracy: 0.9837 - val_loss: 0.0425 - val_accuracy: 0.9880 Out[24]: [0.039418088585138324, 0.9860000610351562]
Ecco gli andamenti della funzione di costo (loss) e l’accuratezza:
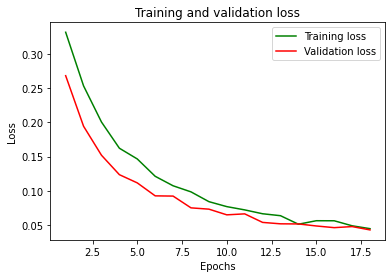
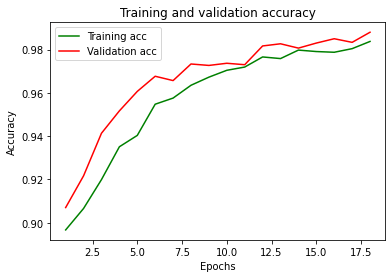
Conclusioni: niente male come accuratezza e loss!
Abbiamo dovuto lavorare un po’ sui vari parametri della CNN per ottenere questi risultati.
Proviamo l’inferenza andando a predire uno dei messaggi registrati nel dataset di test.
#Print the sound to be predicted
sound_index = 10
y_test[sound_index]
array([0, 0, 0, 0, 0, 0, 1, 0, 0, 0], dtype=uint8)
Si tratta in questo caso del numero sei.
Ecco la predizione effettuata con il modello realizzato:
pred = model.predict(x_test[sound_index].reshape(-1,size,13,1))
print(“\n\033[1mPredicted digit sound: %.0f”%pred.argmax(),”\033[0m \n “)
print(“Predicted probability array:”)
print(pred)
Predicted digit sound: 6 Predicted probability array: [[3.8950305e-02 9.8831032e-04 7.7098295e-02 8.1201904e-02 2.2223364e-03 4.8808311e-04 6.2295502e-01 1.0375674e-03 1.6901042e-01 6.0477410e-03]]
Il nostro modello neurale di intelligenza artificaile per riconoscimento vocale ha predetto correttamente il valore sei con probabilità pari a circa 0.623.
Il secondo valore più vicino a questa predizione è il numero otto, con probabilità pari a circa 0.169.
Ovviamente per affinare meglio il nostro codice andremo a salvare il modello di apprendimento (ad esempio su disco) per poi utilizzarlo online durante la fase di predizione, che deve essere rapida per la nostra applicazione di speech recognition.
Volete approfondire meglio questi argomenti?
Ecco una lettura interessante su Machine Learning e AI.