In questo primo articolo giocheremo con la regressione lineare con l’obiettivo di prendere confidenza su alcuni concetti chiave relativi al machine learning.
Le reti neurali convoluzionali, le reti neurali ricorrenti, gli algoritmi di SVN, e di regressione logistica sono ottime tecniche per realizzare predizioni su dati estremamente complessi, compresi quelli che possiedono caratteristiche non lineari.
Tuttavia, la regressione lineare è un ottima soluzione per effettuare delle predizioni su dati che presentano correlazioni lineari.
Consideriamo un set di dati relativo ad alcuni atleti australiani raccolti in uno studio di qualche tempo fa, per verificare come le varie caratteristiche del sangue cambiavano al variare dellla corporatura sportiva dell’atleta. Questi dati sono stati la base per le analisi riportate da Telford e Cunningham nel 1991.
Chiunque sia interessato a conoscere meglio lo studio in esame può fare riferimento a Telford, R.D. e Cunningham, R.B. 1991: sesso, sport e dipendenza dell’ematologia dalle dimensioni corporee in atleti altamente allenati. Medicina e scienza nello sport 23: 788-794:
https://europepmc.org/article/med/1921671
Utilizzeremo il linguaggio Python con l’ambiente Jupyter Notebook per realizzare questo modello di machine learning.
Importiamo alcune librerie utili per iniziare:
from sklearn.metrics import classification_report
from sklearn import metrics
import pandas as pd
import statsmodels.api as sm
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
Importiamo quindi il nostro dataset con i dati aggregati (e ovviamente anonimi) sugli atleti:
#Import dataset inside the dataframe df
df = pd.read_csv(‘http://gosmar.eu/ml/ais.csv’, index_col=0)
print(df.head(2))
print(“Lenght:”, len(df_male))
Analizziamo le features (ovvero le colonne) di questo dataset:
rcc wcc hc hg ferr bmi ssf pcBfat lbm ht wt sex sport
1 3.96 7.5 37.5 12.3 60 20.56 109.1 19.75 63.32 195.9 78.9 f B_Ball
2 4.41 8.3 38.2 12.7 68 20.67 102.8 21.30 58.55 189.7 74.4 f B_Ball
Lenght: 102
Le feature spaziano dall’ematocrito al ferro, alle diverse tipologie di massa corporea, peso, altezza, tipologia di sport e altro ancora.
In questo esempio desideriamo mantenere semplice il nostro modello, selezioniamo quindi solo due feature al fine di implementare una regressione lineare su due dimensioni: la prima sarà la nostra variabile indipendente, la seconda sarà il valore da prevedere (denominata anche target label).
Cerchiamo due feature con una correlazione significativa tra di loro.
Un buon modo per valutare la correlazione tra le colonne è stampare la heatmap!
import seaborn as sns; sns.set()
fig, ax = plt.subplots(figsize=(14,10))
ax = sns.heatmap(df.corr(), cmap=”YlGnBu”, annot = True)
Ecco il risultato:
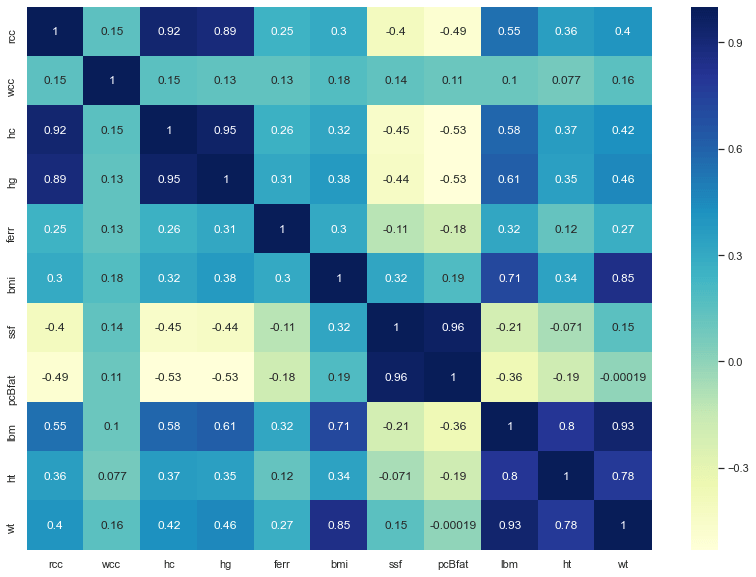
Più il colore delle caselle risulta scuro, più le due feature corrispondenti saranno correlate, quindi selezioneremo per il nostro esempio le seguenti:
X (variabile indipendente) = bmi
Y (target label da predire) = lbm
Dove bmi è acronimo di Body Mass Index, in kg e lbm sta per Lean Body Mass, in kg.
Ovvero Indice di Massa Corporea e Indice di Massa Magra: due parametri particolarmente importanti per atleti di alto livello.
Effettuiamo ora un po’ di feature engineering iniziando con operazioni di dimensionality reduction. Paroloni in gergo ML 😉
In termini semplici: rimuoviamo alcune delle colonne che non ci servono!
df_new=df.drop(['rcc','hc','hg','ferr','ssf','pcBfat','sport'], axis=1)
print(df_new.head(6))
print(len(df_new))
result: wcc bmi lbm ht wt sex 1 7.5 20.56 63.32 195.9 78.9 f 2 8.3 20.67 58.55 189.7 74.4 f 3 5.0 21.86 55.36 177.8 69.1 f 4 5.3 21.88 57.18 185.0 74.9 f 5 6.8 18.96 53.20 184.6 64.6 f 6 4.4 21.04 53.77 174.0 63.7 f 202
Separiamo i dati in due dataframe: il primo con dati maschili, il secondo con quelli femminili.
df_male = df_new.loc[df_new.sex == ‘m’]
print(df_male.head(2))
print(“Lenght:”, len(df_male))
result: wcc bmi lbm ht wt sex 101 7.1 22.46 61.0 172.7 67.0 m 102 7.6 23.88 69.0 176.5 74.4 m Lenght: 102

df_female = df_new.loc[df_new.sex == ‘f’]
print(df_female.head(2))
print(“Lenght:”, len(df_female))
result:
wcc bmi lbm ht wt sex
1 7.5 20.56 63.32 195.9 78.9 f
2 8.3 20.67 58.55 189.7 74.4 f
Lenght: 100
Impostiamo ora la variabile indipendente (bmi) e la target label (lbm) per predisporre la fase di training ovvero di apprendimento dell’algoritmo che andremo ad adottare:
#To_be_predicted
y1_male = df_male[‘lbm’]
#Intependent vars
X1_male = df_male[‘bmi’]
#Add constant to better fit the linear model
X1_male = sm.add_constant(X1_male.to_numpy())
Utilizziamo la libreria statsmodels.regression.linear_model.OLS per implementare il nostro modello di regressione lineare:
model = sm.OLS(y1_male, X1_male)
E’ giunto il termine dell’apprendimento vero e proprio ovvero la procedura di fitting, nella qualche andiamo ad adattare il modello di machine learning con il nostro dataset di training per ottenere quella che chiameremo la learned function: la funzione che utilizzeremo in seguito per la fase di predizione vera e propria (o inferenza).
model = model.fit()
Ora proviamo a visualizzare i dati di training cioè la lmi in funzione della bmi che otterremo dal nostro set di dati importato e dalla funzione di regressione lineare relativa al modello appena creato. In questo caso sarà una retta di tipo: Y = c1 + c2X.
Usiamo alcune opzioni di visualizzazione matplotlib per questa operazione:
#Create the X array from the min to the max observations
X_obs = np.linspace(X1_male[:,1].min(), X1_male[:,1].max(), len(df_male))[:, np.newaxis]
X_obs = sm.add_constant(X_obs)
#Let’s calculate the predicted values
y_pred = model.predict(X_obs)
fig = plt.figure()
fig.subplots_adjust(top=3.8, right = 1.9)
ax1 = fig.add_subplot(211)
plt.scatter(X1_male[:,1], y1_male, alpha=0.3) # Plot the raw data
plt.title(“Linear Regression (male)”, fontsize=20)
plt.xlabel(“Body mass index, kg”, fontsize=20)
plt.ylabel(“Lean body mass, kg”, fontsize=20)
plt.plot(X_obs[:, 1], y_pred, ‘g’, alpha=0.9) # Add the regression line, colored in red
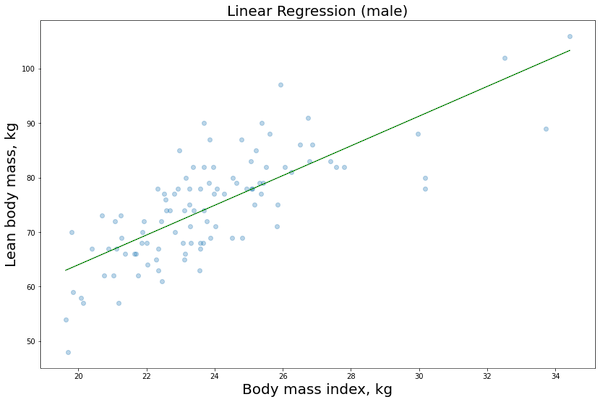
Ripentiamo quindi la stessa procedura per i dati femminili:
#To_be_predicted
y1_female = df_female[‘lbm’]
#Intependent vars
X1_female = df_female[‘bmi’]
#Add constant to better fit the linear model
X1_female = sm.add_constant(X1_female.to_numpy())
model = sm.OLS(y1_female, X1_female)
model = model.fit()
#Create the X array from the min to the max observations
X_obs = np.linspace(X1_female[:,1].min(), X1_female[:,1].max(), len(df_female))[:, np.newaxis]
X_obs = sm.add_constant(X_obs)
#Let’s calculate the predicted values
y_pred = model.predict(X_obs)
fig = plt.figure()
fig.subplots_adjust(top=3.8, right = 1.9)
ax1 = fig.add_subplot(211)
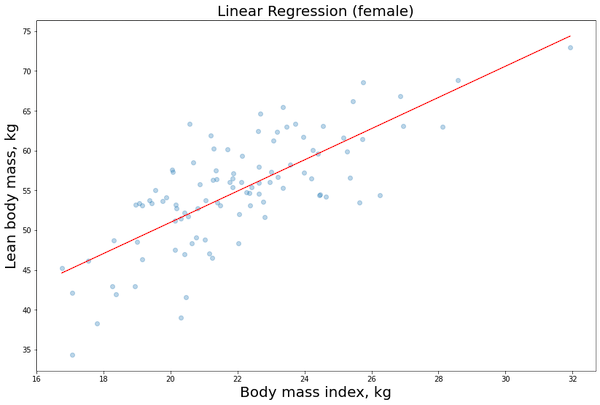
plt.scatter(X1_female[:,1], y1_female, alpha=0.3) # Plot the raw data
plt.title(“Linear Regression (female)”, fontsize=20)
plt.xlabel(“Body mass index, kg”, fontsize=20)
plt.ylabel(“Lean body mass, kg”, fontsize=20)
plt.plot(X_obs[:, 1], y_pred, ‘r’, alpha=0.9) # Add the regression line, colored in red
Ora che abbiamo adattato e costruito il nostro modello (fase di addestramento o fitting), andremo a valutare alcuni risultati per capire se sia utile cambiare qualcosa sull’algoritmo e sui cosiddetti iperparametri (fase di validazione):
model.summary()
| Dep. Variable: | lbm | R-squared: | 0.559 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.554 |
| Method: | Least Squares | F-statistic: | 124.1 |
| Date: | Sun, 10 May 2020 | Prob (F-statistic): | 4.15e-19 |
| Time: | 19:24:20 | Log-Likelihood: | -293.96 |
| No. Observations: | 100 | AIC: | 591.9 |
| Df Residuals: | 98 | BIC: | 597.1 |
| Df Model: | 1 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 11.7975 | 3.896 | 3.028 | 0.003 | 4.065 | 19.530 |
| x1 | 1.9599 | 0.176 | 11.140 | 0.000 | 1.611 | 2.309 |
| Omnibus: | 1.486 | Durbin-Watson: | 1.327 |
|---|---|---|---|
| Prob(Omnibus): | 0.476 | Jarque-Bera (JB): | 1.345 |
| Skew: | -0.282 | Prob(JB): | 0.510 |
| Kurtosis: | 2.934 | Cond. No. | 187. |
I valori che ci interessano maggiormente per le nostre valutazioni sulla bontà del modello sono i seguenti:
- R2 (compreso tra zero e uno): più è vicino allo zero, meno i coefficienti (nel nostro caso c1, c2) della funzione lineare sono in grado di spiegare il modello e la varianza dei dati di training. L’obiettivo è avere R2 più alto possibile.
- R2 adjusted: è utilizzato quando abbiamo a che fare con regressioni lineari in presenza di più di una variabile indipendente, ad esempio se oltre a valutare lmi in funzione di bmi, avessimo usato anche l’altezza (ht) e il peso totale dell’atleta (wt): in questo caso saremo stati di fronte ad una funzione tipo Y = c1 + c2X + c3W + c4Z + …
- Prob (F-statistic): funzione di probabilità utilizzata come metodologia per il calcolo del valore p (p-value in gergo). L’obiettivo è avere dei valori p più bassi possibili. p-value bassi sono indicatori che il coefficiente di riferimento è affidabile per spiegare le variazioni dei dati ovvero è affidabile per il nostro modello in termini statistici (la cosiddetta ipotesi nulla è improbabile).
Abbiamo visto che il nostro modello lineare di esempio è bidimensionale, ovvero:
Y = c1 + c2X.
Con questo comando possiamo agevolmente mostrare c1 e c2:
model.params
result: const 11.797524 x1 1.959934
…Dove c1 = const e c2 = x1
Per mostrare invece i valori p relativi ai due coefficienti c1 e c2, usiamo questo metodo:
print(model.pvalues)
const 3.147591e-03 x1 4.150618e-19
Affinché i coefficienti siano statisticamente adeguati, impostiamo una soglia (normalmente compresa tra 0.05 e 0,01). Valori p superiori a questa soglia indicano che il coefficiente relativo non è affidabile per rappresentare la varianza dei dati.
Possiamo facilmente dimostrare che c1 è l’intersezione della linea retta con l’asse Y, mentre c2 è la pendenza della linea retta (la sua derivata per i matematici).
Nel nostro caso abbiamo che c1 è piuttosto affidabile e c2 risulta molto affidabile!
Conclusioni:
Abbiamo utilizzato un set di dati per risolvere un problema di regressione, quindi per prevedere un valore (non una categoria sia ben inteso, altrimenti avremmo affrontato un problema di classificazione).
Per prima cosa abbiamo eseguito una pre-elaborazione del set di dati (sempre utile prima di prendere in considerazione qualsiasi tipo di algoritmo): abbiamo identificato le caratteristiche (features o colonne) che presentavano correlazioni più interessanti utilizzando la funzione heatmap e abbiamo eseguito alcune riduzioni dimensionali per eliminare le funzioni non utili alla nostra analisi.
Dopo questa fase inziale, siamo quindi passati agli step di training (apprendimento) e validation (validazione) così da scegliere il modello e addestrarlo (fitting)
Infine abbiamo mostrato i coefficienti della funzione lineare ottenuti (c1, c2) e valutato la bontà del modello utilizzando alcuni parametri utili in caso di regressione lineare: R2 e i valori p.
Vuoi approfondire questi argomenti?
Ecco una lettura interessante su Machine Learning e AI.


