Abbiamo già visto in questo post precedente un esempio di regressione lineare semplice, ovvero un set di algoritmi e tecniche per machine learning in grado di predire una variabile di output data una sola variabile indipendente, quindi tramite una funzione lineare Y = c1 + c2X.
Oggi vediamo invece la sua estensione, ovvero come predire Y in funzione di più variabili indipendenti lineari (X1, X2, X3 etc… etc…). Questa tipologia di modelli prende anche il nome di regressione lineare multipla.
Riutilizziamo il dataset relativo alle analisi del sangue effettuate alcuni anni fa su atleti professionisti australiani in varie discipline sportive: riferimento Telford, R.D. e Cunningham, R.B. 1991 – sesso, sport e dipendenza dell’ematologia dalle dimensioni corporee in atleti altamente allenati. Medicina e scienza nello sport 23: 788-794.
Il dataset in questione contiene 13 feature relative a 202 osservazioni.
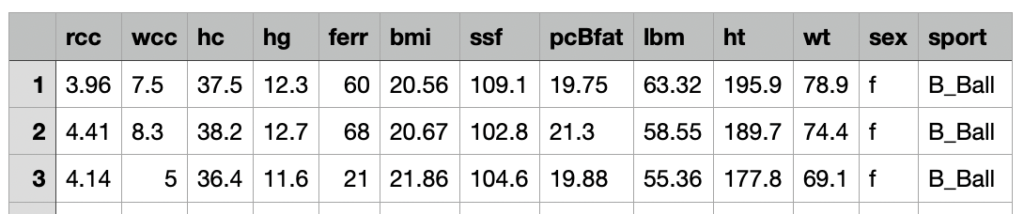
Ecco la descrizione delle feature:
rcc: numero globuli rossi [in]
WCC: numero globuli bianchi [in per liter]
hc: ematocrito, percentuale
hg: concentrazione di emoagglobina,
ferr: ferritine plasmatiche, ng
bmi: indice di massa corporea, kg
ssf: calibro delle pieghe cutanee
pcBfat: percentuale di grasso corporeo
LBM: indice di massa magra, kg
HT: altezza (cm)
wt: peso (Kq)
sesso: maschio/femmina
sport: B_Ball Campo Palestra Netball Row Nuotata T_400m T_Sprnt Tennis W_Polo
Nel questo post precedente abbiamo utilizzato il modello di regressione lineare per stimare la labeled feature LBM in funzione della variabile indipendente bmi (regressione semplice). Abbiamo utilizzato il seguente stimatore fornito da scikit-learn:
model = sm.OLS(y, X)
…E abbiamo così ottenuto le rette di regressione relative alle nostre predizioni.
Rivediamo qui di seguito quelle per gli atleti femminili:
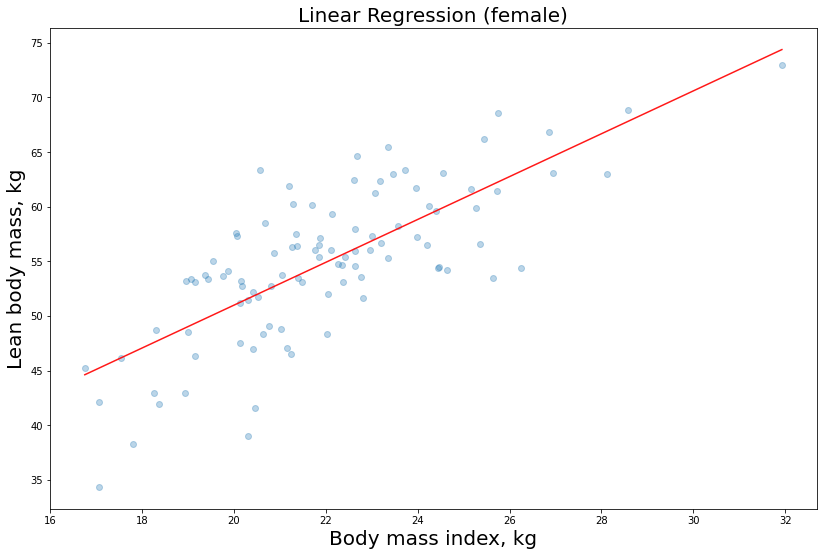
Ora proviamo a impostare lo stesso modello, ma questa volta usiamo due variabili indipendenti, ovvero X1 = bmi e X2 = wt, per predire la nostra y=LBM
Procediamo con la fase di training:
To_be_predicted
y1_male = df_male[‘lbm’]
Intependent vars
X1_male = df_male[[‘bmi’,’wt’]]
Add constant to better fit the linear model
X1_male = sm.add_constant(X1_male.to_numpy())
model = sm.OLS(y1_male, X1_male)
model = model.fit()
Vediamo i risultati di accuratezza, R2 e p-value:
model.summary()
| Dep. Variable: | lbm | R-squared: | 0.949 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.948 |
| Method: | Least Squares | F-statistic: | 917.8 |
| Date: | Fri, 15 May 2020 | Prob (F-statistic): | 1.25e-64 |
| Time: | 12:59:17 | Log-Likelihood: | -226.33 |
| No. Observations: | 102 | AIC: | 458.7 |
| Df Residuals: | 99 | BIC: | 466.5 |
| Df Model: | 2 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 15.6579 | 1.968 | 7.956 | 0.000 | 11.753 | 19.563 |
| x1 | -0.5647 | 0.148 | -3.820 | 0.000 | -0.858 | -0.271 |
| x2 | 0.8785 | 0.033 | 26.641 | 0.000 | 0.813 | 0.944 |
| Omnibus: | 26.701 | Durbin-Watson: | 1.686 |
|---|---|---|---|
| Prob(Omnibus): | 0.000 | Jarque-Bera (JB): | 56.728 |
| Skew: | -0.995 | Prob(JB): | 4.80e-13 |
| Kurtosis: | 6.064 | Cond. No. | 765. |
Questa volta il parametro Adjusted R-square è significativo, perchè abbiamo a che fare con una regressione lineare multipla. Ricordiamoci che se R tende a zero significa che il nostro modello non spiega bene i dati di training, mentre più si avvicina ad uno, più i coefficienti lineari sono in grado di seguire le osservazioni.
0.948 è ovviamente un ottimo risultato!
Possiamo stampare i nostri coefficienti e il p-value:
print(“linear coefficients:\r”,model.params)
print(“p-value:\r”,model.pvalues)
const 15.657902: x1 -0.564722 x2 0.878512 const 2.975861e-12 x1 2.326238e-04 x2 6.007130e-47
I p-value sono tutti e tre sotto lo 0.01 quindi i nostri coefficienti risultano statisticamente affidabili per seguire le variazioni dei dati.
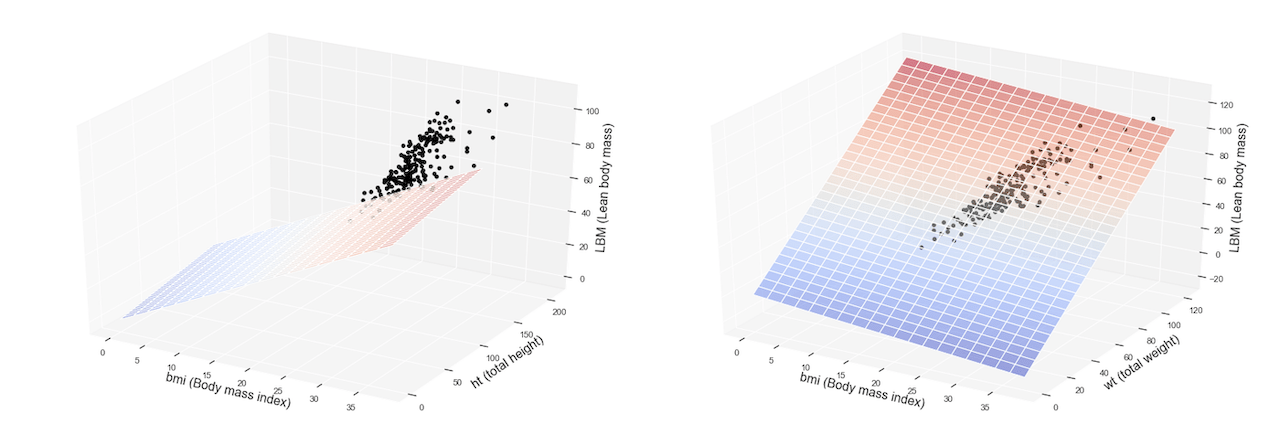
Ora desideriamo visualizzare graficamente il nostro modello. Siccome abbiamo due variabili indipendenti, questa volta il grafico non sarà una semplice retta, ma una superficie ovvero un piano in uno spazio a tre dimensioni.
Ecco come possiamo stampare il modello di regressione multipla (per semplicità non abbiamo suddiviso i dati tra maschi e femmine in questo caso):
Rispetto all’esempio di regressione semplice importiamo due librerie aggiuntive:
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
Procediamo quindi alla predisposizione e visualizzazione del nostro grafico per la regressione lineare multipla:
df = pd.read_csv(‘http://gosmar.eu/ml/ais.csv’, index_col=0)
#To_be_predicted
y = df[‘lbm’]
#Intependent vars
X = df[[‘bmi’,’wt’]]
model=sm.OLS(y, X)
fit = model.fit()
fit.summary()
fig = plt.figure()
fig.subplots_adjust(top=2.0, right = 2.0)
ax = fig.add_subplot(111, projection=’3d’,facecolor=’white’)
x_surface = np.arange(0, 40, 2) # generate a mesh
y_surface = np.arange(0, 124, 4)
x_surface, y_surface = np.meshgrid(x_surface, y_surface)
exog = pd.core.frame.DataFrame({‘bmi’: x_surface.ravel(), ‘wt’: y_surface.ravel()})
out = fit.predict(exog = exog)
ax.plot_surface(x_surface, y_surface,
out.values.reshape(x_surface.shape), cmap=cm.coolwarm,
rstride=1,
cstride=1,
color=’none’,
alpha = 0.5)
ax.scatter(df[‘bmi’], df[‘wt’], df[‘lbm’],
c=’black’,
marker=’o’,
alpha=1)
ax.set_xlabel(‘bmi (Body mass index)’,fontsize=16)
ax.set_ylabel(‘wt (total weight)’, fontsize=16)
ax.set_zlabel(‘LBM (Lean body mass)’, fontsize=16)
plt.show()
Ecco il nostro risultato!
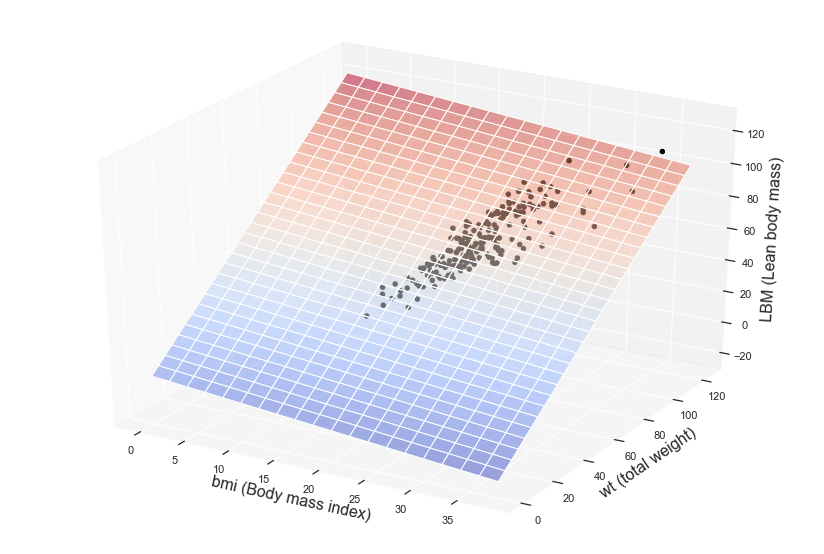
Il piano colorato rappresenta il nostro modello di regressione multipla, ovvero le predizioni o inferenze mentre i puntini sono relativi alle osservazioni disponibili nel dataset di training.
Vuoi approfondire questi argomenti?
Ecco una lettura interessante su Machine Learning e AI.